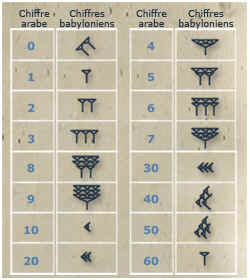
Ce sont les Babyloniens qui vont les premiers utiliser le zéro (vers le 3e siècle après J.-C.), non pas comme un nombre ni même un chiffre, mais en tant que marqueur signifiant l'absence. Par exemple, si l'on voulait transposer le nombre 507 par écrit, on écrivait 5 7 ; il y avait 5 centaines, aucune dizaine et sept unités. Pour se rappeler cette absence et éviter un confusion avec le nombre 57, les scribes (et non les mathématiciens) inventèrent un marquage prenant la forme d'un double chevron pour signifier cette absence.

Fondamentalement, ce sont les savants indiens qui vont faire évoluer le zéro vers le sens que nous lui reconnaissons aujourd'hui, à savoir d'un nombre entier non naturel, pair, ni premier, ni positif, ni négatif. Dans la philosophie hindoue, le vide et l'infini sont dans l'essence même du cosmos, aussi le zéro va-t-il devenir un nombre à part entière. Il sera défini comme la soustraction d'un nombre par lui-même (x - x = 0). Le zéro est alors appelé sunya ce qui signifie le vide. Au 12e siècle, le mathématicien indien Bhaskara parvient à établir que 1/0 = l'infini. Il démontre ainsi, la relation qui existe entre le vide et l'infini.

Au 9e siècle, les Arabes emprunteront aux Indiens le zéro, le mot sunya devenant sifr. Ce ne sera finalement qu'au 12e siècle que le nombre arrivera en Occident, le mot devenant zefiro pour devenir zéro à la fin du 15e siècle.

sommaire

L'histoire de "un"

Evolution de la transcription du chiffre 1

L'histoire du nombre Pi va consister à approcher au plus juste sa valeur, en cherchant toujours plus de décimales.

En 1800 avant J.-C., les Egyptiens approchent, d'après le calcul de disque et de carré sur le papyrus Rhind, le nombre 3,16 pour Pi. Les Babyloniens arrivent en 900 avant J.-C. au nombre de 3,125.

C'est à Archimède de Syracuse (282-212 avant J.-C.) que nous devons l'approximation qui encadre Pi autour de 3+(10/71) et 3+(1/7). Il procède par une méthode consistant à encadrer un cercle par des polygones dont on connaît la surface de façon précise afin d'estimer au mieux un encadrement de Pi.

L'histoire de Pi se prolonge de continent en continent (depuis les travaux du Chinois Liu Hui en allant jusqu'à ceux d'Isaac Newton en passant par l'astronome perse Massoud al Kashi), de siècle en siècle, avec un nombre de décimales toujours plus conséquent. C'est au 18e siècle qu'Euler établira de façon définitive la notation Pi, en référence au mot grec périmètre qui signifie circonférence.

Quoiqu'il en soit, même si les travaux démontrent toujours une plus grande connaissance quantitative de Pi, nous ignorons toujours pourquoi cette constante existe.

Pour comprendre ce nombre irrationnel, il est utile tout d'abord de comprendre l'histoire de l'émergence de son besoin.

Au 16e siècle, il n'existe ni ordinateur ni calculatrice. Or, les sociétés occidentales dans leur course à la maîtrise des océans, dans l'émergence des transactions boursières ou encore dans l'étude des astres, ont besoin de calculs de plus en plus précis.

Dans cette optique, un mathématicien écossais du nom de John Napier (John Neper en français) entreprend pendant 20 ans, de réaliser des tables de calculs qui simplifieraient les opérations complexes. Il pose ainsi les bases du calcul logarithmique en 1617. L'un des systèmes de calcul logarithmique sera le logarithme népérien (noté ln).

Les logarithmes sont des nombres artificiels utilisés pour obtenir le résultat de l'opération. Ils servent d'intermédiaires. Cependant, ces nombres intermédiaires sont transcendants, et, de la même manière que pour le nombre Pi des siècles auparavant, les mathématiciens vont faire émerger un symbole qui permettra de nommer en une lettre une infinité de chiffres, c'est le nombre e. Ainsi ln(e) = 1.

Même s'il sera étudié par Leibniz, Huygens ou encore Bernoulli, le nombre e sera nommé conventionnellement par le mathématicien Suisse Leonhard Euler (1707-1783) qui attribuera cette lettre en rapport, non pas avec son nom, mais avec la fonction exponentielle qu'elle décrit.

Longtemps réduite par les historiens à l'expression d'une menace pour l'Occident médiéval, la civilisation arabo-musulmane qui s'épanouit entre le 7e et le 15e siècle du Moyen-Orient à l'Espagne, est aujourd'hui reconnue dans l'histoire des idées par les échanges qu'elle a permis et ses nombreux apports scientifiques.

Le premier rôle est donc un rôle de transmission des savoirs.

Tout d'abord, les Arabes vont permettre aux mathématiques de garder la trace des avancées de l'Antiquité. Sans eux, toutes les découvertes des Pythagoriciens ou d'Euclide par exemple, auraient été perdues dans l'effondrement de l'Empire romain.

Transmission de savoirs ensuite entre l'Occident et l'Orient. A travers des échanges culturels intenses avec les centres intellectuels indiens ou occidentaux (comme la Sicile au 12e siècle), les Arabes vont ainsi, notamment, introduire les fameux chiffres arabes à partir de l'Inde vers l'Occident. Durant tout le Moyen Age, les civilisations arabo-musulmanes seront les plaques tournantes des savoirs mathématiques et astronomiques.

Les Arabes n'ont pas seulement échangé des informations, ils ont aussi contribué grandement à l'histoire des mathématiques à travers de brillants mathématiciens.

Al Khawarizmi ayant vécu au 9e siècle signe le premier traité d'algèbre (al jabr en arabe). En plus d'innovations en trigonométrie (avec l'usage du sinus) ou dans la résolution d'équations du second degré. Sa mémoire perdure avec le mot algorithme, qui est dérivé de son nom.

Abu Al-Wafa, mathématicien perse du 10e siècle, illustre également les avancées scientifiques de cette époque. Il établit un nouveau concept en trigonométrie avec la tangente et aussi la sécante.

Après les progrès de la Renaissance dans le domaine du calcul intégral, l'Occident va se découvrir un intérêt extraordinaire pour les mathématiques au 17e siècle. Un mouvement formidable de découvertes et de créations va se structurer autour de grands mathématiciens de génie. Les mathématiques modernes résultent, dans leurs méthodes et dans leurs notations, en grande partie des avancées de cette époque.

A côté de Huygens, Kepler et autres Torricelli, cinq grandes figures dominent ce siècle.

René Descartes (1596-1650) s'impose tout d'abord par sa méthode qui prône un raisonnement fondamentalement hypothético-déductif. Ses travaux ensuite ouvrent la voie à la géométrie projective et à la géométrie analytique.

On lui doit également de nombreuses notations d'algèbre encore employées aujourd'hui : x,y,z pour des inconnues, les exposants pour les puissances sous la forme xⁿ ou encore les paramètres a,b,c.

Pierre Simon de Fermat (1601-1665) est un mathématicien français comme Descartes. Il est connu surtout par sa fameuse conjecture qui va passionner 350 années de recherches en mathématiques. Parmi ses nombreuses contributions, citons l'introduction de la démonstration par l'absurde, du calcul de probabilités, des combinatoires, des calculs des dérivés et surtout ses nombreux travaux sur la théorie des nombres.

Blaise Pascal (1623-1662), mathématicien, physicien ou encore philosophe apparaît comme l'un des plus grands génies de l'histoire de France. A 12 ans, il parvenait déjà à démontrer les théorèmes de la géométrie classique. Avant ses 19 ans, il avait rédigé un traité sur les coniques et mis au point une machine à calculer ! Il ouvrira la voie aux calculs infinitésimaux, à l'intégration, aux calculs de probabilités et à l'analyse combinatoire.

Au fil de l'histoire, les mathématiciens ont progressivement pris conscience qu'il existait une infinité de nombres, de natures très variées. Ils se sont aperçus qu'il était possible de "ranger" en grandes familles les nombres ayant des propriétés identiques.

Cette typologie fut l'oeuvre de trois mathématiciens de la deuxième moitié du 19e siècle et du début du 20e siècle : l'Allemand Richard Dedekind (1831-1916), le Russe Georg Cantor (1845-1918) et l'Italien Giuseppe Peano (1858-1932).

L'ensemble N vient de l'appellation naturale attribuée à Peano. Il désigne l'ensemble des nombres entiers naturels (exemples : 0 1 2 3 7). Si l'on note N, cela signifie que l'on exclut le zéro.

L'ensemble Z vient de l'allemand zahlen qui signifie compter. Ainsi défini par Dedekind, il recouvre l'ensemble des nombres entiers relatifs (exemples : -3 -1 0 1 5). N appartient à Z.

L'ensemble Q a été défini par Peano, il vient de l'italien quotiente (la fraction). Il définit l'ensemble des nombres rationnels (exemples : -3 -2,5 0 1,25 1/3 2,666). Le nombre peut être décimal limité (3/4 = 0,75) ou périodique (2/3 = 0,666). Z appartient à Q.

L'ensemble R, défini par Dedekind, pour real, recouvre les nombres réels. Cela comprend les nombres dits algébriques, c'est-à-dire ceux qui peuvent s'exprimer par une égalité simple (les fractionnaires périodiques, comme les nombres irrationnels) et les nombres dits transcendants (ceux qui ne peuvent s'exprimer par une égalité simple). Exemples de nombres réels : -1/3 0 Pi e √2. Q appartient à R.

Il existe d'autres ensembles : C pour les nombres complexes, H pour les hypercomplexes, O pour les Octavions, Q_p pour le nombre p-adiques. Leur utilisation est requise pour les applications plus poussées en dynamique des fluides, en physique nucléaire ou pour les géométries non-euclidiennes.

sommaire

Le système métrique est l'expression d'un moment historique qui a conduit les mathématiciens à intervenir dans les systèmes de mesure quotidienne. Tout a commencé en France, lors de la rédaction des cahiers de doléances en 1789. Le clergé, la noblesse et le tiers état se sont accordés au moins sur un point, à savoir le besoin d'une unification des poids et des mesures.

Le 8 mai 1790, l'Assemblée nationale vota la création d'un système de mesure sur une base décimale. Le principe était que ce système délivre une information stable, simple et équivalente.

Par décret, l'unité de base fut le mètre, défini comme la dix millionième partie du quart du méridien terrestre (entre le Pôle et l'équateur). Pour la calculer, la Convention donna à deux astronomes, Delambre et Méchain, la tâche de mesurer le méridien entre Dunkerque et Barcelone via Rodez.

Le mètre ainsi calculé allait devenir la norme légale et obligatoire pour la France, bientôt jointe par les pays envahis par Napoléon.

De nombreuses redéfinitions du mètre auront lieu même s'il ne changera pas de nature. En 1889, le Bureau international des poids et mesures redéfinit le mètre comme étant la distance entre deux points sur une barre étalon composé d'un alliage de platine-iridium. En 1960, à l'aide de la technologie des lasers, la Conférence générale des poids et mesures définit le mètre comme 1 650 765,73 longueurs d'onde d'une radiation orangée émise par l'isotope 86 du krypton.

On associa à la mesure de la longueur (le mètre), les mesures des superficies (en are), des masses (en gramme), des pressions (en bar puis en pascal), des intensités (en ampère), des températures (en degrés Kelvin ou Celsius), du temps (en seconde) et des volumes (en litre).

Pour les multiples, on utilisa des préfixes grecs (déca-, hecto-, kilo-, myria-, méga-, giga-). Pour les fractions, des préfixes latins (déci-, centi-, milli-). La quasi-totalité des pays ont adopté le système métrique de façon légale, même si des réticences culturelles retardent une utilisation complète.

Il est intéressant de noter que ce système reste le résultat d'une abstraction du réel et non le réel lui-même, le mètre n'existe pas ailleurs que dans l'esprit humain !

sommaire